LineArt

Link to code and image library

This is a very simple algorithm for converting images to a set of linear line segments. Below we will see how we can use it to make abstract bird art.

Logic Overview

We start by running our input image through a Canny filter so we can detect a wide variety of edges. We can modify the threshold (sigma) of this filter to preserve varying levels of detail in our final output image. In this project, we will use sigma values from 1 to 5. Examples are further down this page.

We can break any of these edge map images im up into a series of NxN pixel squares, which we will call image segments. In this project, we use numpy for this as follows:

for i in range(im.shape[0]-N):
  for j in range(im.shape[1]-N):
    if make_sparse and (i%N > 0 or j%N > 0): continue
    im_seg = im[i:i+N,j:j+N]

The make_sparse flag on line 3 controls whether we want the filter's output to have attempted line generation for every possible NxN square, or if we only want to check a grid of squares. The impact of this choice is shown in further detail below.

For each of these image segments, we attempt to find a line that properly represents its content. That entails the following 2 things:

  1. The center pixel, [N/2,N/2], is an edge.
  2. Edge pixels span either the horizontal or vertical axis (or both). We define spanning an axis X as having edge pixels on either side (relative to X) of the center pixel.
If those things are true, then we calculate the linear regression line for all the edge pixels of the image segment. (Aside: One weakness of this technique is that perfectly vertical lines cannot be captured. A solution could be to calculate a line for each image segment's transpose and `&` it with the other line) We drop the y-intercept and use only the slope, because we are readjusting our line to go through the center pixel of the image segment. These slopes are cached (using the image segment as a key) so we never need to do the calculation more than O(2^N^2) times.

Finally, we draw our line on the canvas that will eventually be our output image. As mentioned above, we draw a line with the calculated slope through the center of the image segment. The length of the line is given by (roughly) N^2.

Examples

Below we have the output of applying this filter witih a variety of parameters to this image of a bird:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image of a bird:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image of a bird:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image of a racoon:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image of a tree:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image of a fox:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Below we have the output of applying this filter witih a variety of parameters to this image:

Sparse

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

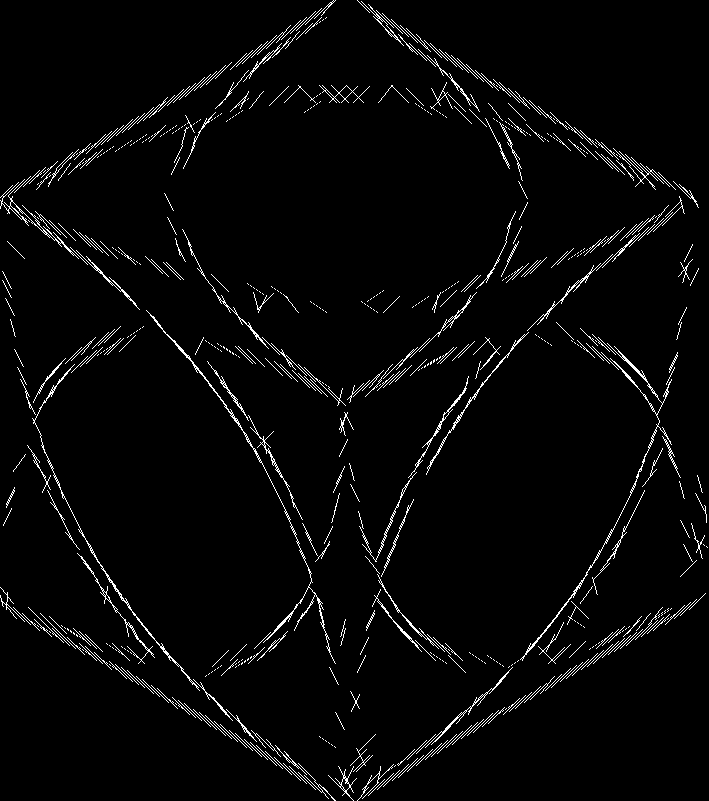
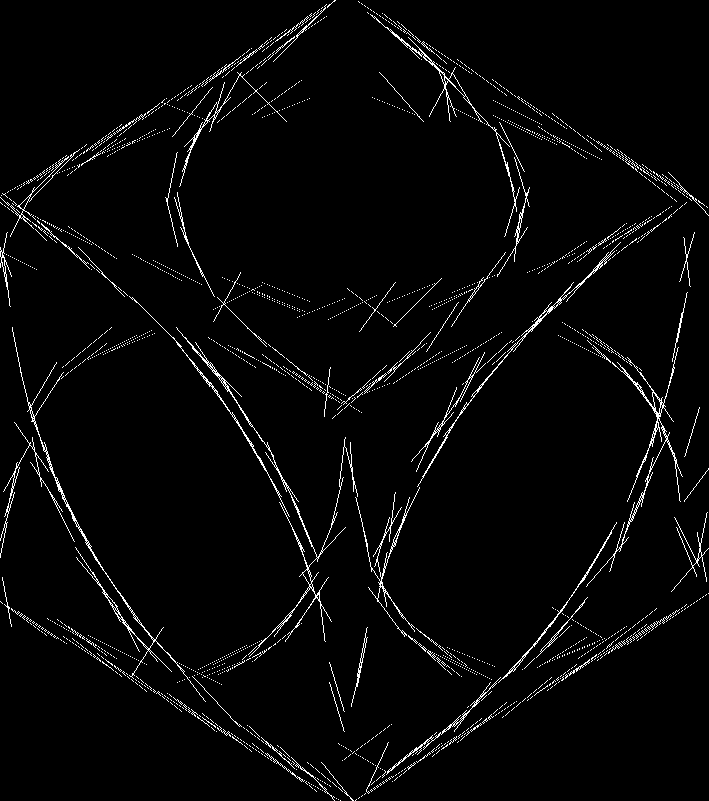
Below we have the output of applying this filter witih a variety of parameters to this image. This set is a good demonstration of the weaknesses of the linear regression method:

  1. We cannot have perfectly vertical lines.
  2. We cannot guarantee preservation of density of lines, since image segments that would best be represented with multiple lines will always be represented with a single one.
  3. We cannot preserve curved lines. This is arguably an intended feature, since it adds to the "sketchy" effect when applied to organic images. However, as seen below, this is non-ideal in cases where precision and whitespace matter.

Sparse

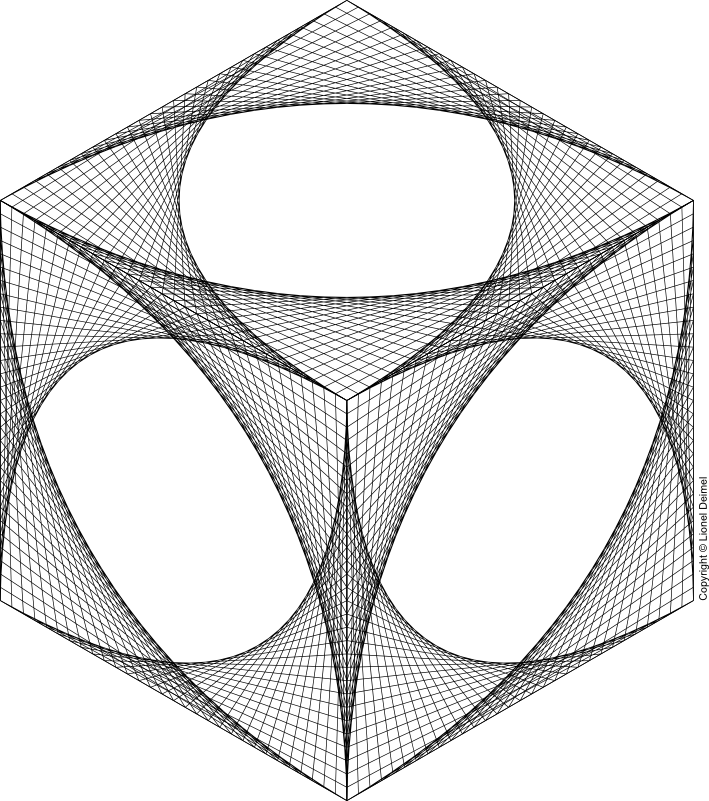
Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7

Dense

Sigma = 1 Sigma = 2 Sigma = 3 Sigma = 4 Sigma = 5
N=3
N=5
N=7