People have been passing around this article about an 11 year old generating $2 passwords using what is essentially a mapping function from a length 6, base 6 int to some word. Her implementation has some flaws, but word based passwords are an intriguing idea. Let's explore.
The core component of the algorithm was rolling a 6-sided dice 5 times, generating a string of 5 numbers each in range [1,6]. Each of the possible 6^5 strings generated by this process is mapped to a word, using the Diceware Word List. This process is repeated 6 times, to generate a total of 6 words, giving any would-be hacker a hypothesis space of 6^5^6. The notable advantage of this password generation procedure is that it allows the user to memorize fewer "items" (words or characters) to remember their passwords.
The studies backing this up are pretty extensive, but for a quick experiment, try memorizing some 8-digit numbers. Then, try it again remembering each 8-digit number as a series of four 2-digit numbers. If you think the way the average person does, you should have an easier time with the 2-digit numbers. For the naive password generation algorithm, this basically boils down to remembering ["cat", "dog", "owl", "pig", "zebra", "allen"] over 162342325344551455266532111625. Pretty good, right? What's the problem?
There are actually 4 problems (that I have noticed so far).
First, many of the words on the Diceware Word List are actually very uncommon and difficult to remember for a number of reasons. Some words on the list are words, but are so uncommon that most people probably would not remember them. In our improved algorithm, we definitely want to restrict this word list to ones common enough for the average person to remember. Worse, many of the "words" on the list are not actually individual words at all. Some are acronyms, some contain special characters, some are names, some are possessive forms or contractions, some are abbreviations, and some are just completely mysteriously not words (e.g. "a&p", "a's", "aa", "aaa", "aaaa"). Special characters definitely make passwords significantly more secure. However, they should be manually added after the words in the password are decided. They should not be inside individual words because from a memory perspective, they turn the nice single-item word into a many-item list of characters.
Second, the password lengths are not dynamic. The longest words in the Diceware Word List are 6 characters long, which would make the longest possible password 36 characters. There are plenty of places that allow passwords longer than that, so if someone feels comfortable memorizing more than 6 words, they should be allowed to do that within the constraints of the system. Likewise, some sites set a maximum password length lower than 36, which the generator should account for. Also, although the average password is long enough (roughly 25 characters), it is still possible to get a password below the minimum acceptable length, currently 12 characters.
Third, some of the words in the Diceware Word List are homophones. If you skipped that class in second grade, a homophone is a word that is pronounced the same way as another word but spelled differently. For example, "deer", "dear", and "deere" are all in the Diceware Word List. That makes it somewhat more difficult to remember the words in your password, especially if two of the words in your password turn out to be homophones with each other. When selecting words for our list, we should try to only select the most common word for each pronunciation.
Fourth, the mappings in the Diceware Word List take dice rolls as input, so it needs exactly 6^5 words. That means that if the number of easily recalled words is less than 6^5, we need to overgenerate and add words to our list that are difficult to recall. On the other hand, if therea re more than 6^5 words that are easy to recall, we have to lose some number of them, since the system only allows for a size 6^5 vocabulary.
If your would-be hacker knows a word list system was used to generate your password, your password immediately becomes MUCH less secure, because the transition probabilities for characters in English words are not even. For some intuition, we know the theoretical hypothesis space of a length N password containing only letters is 26^N. That means there are 26^N possible passwords of length N. This number being big is what makes some passwords harder to crack, since the brute force way of cracking passwords is essentially to just try all of them. However, we know there aren't any words starting with 2 or more z's and no words ending with 3 or more z's, so we can throw out all those possibilities. Now our hypothesis space is smaller. If we keep doing this for all the structural rules pertaining to English words, we can bring our hypothesis space down to a pretty unreasonably small size. Further, there is an uneven distribution of characters relative to a randomly generated password. You could expect to see a lot more vowels than consonants, for example, so the brute forcing strategy could probably be speed up by prioritizing maybe-passwords with some expected distribution of characters. There are all kinds of ways the patterns in language make passcode strings less secure.
As a result, if you do decide to use this system for password generation, make sure you (1) don't tell anyone about it and (2) add special or nonsense characters to your generated password.
The first step is generating a better list of words. These need to be words that are common and not homophones with each other.
For my list of common words, I cloned this git repo. To get pronunciations, I used CMUDict.
First, I filtered out the capitalized repeat words and words containing special characters from the list of top 100k words. This word list was likely generated using a tokenized (by space, but not by special character) corpus without capitalization preprocessing, so the after removing the repeats, the "common-ness" ordering is not quite correct. For example, "his" and "His" were both present near the top of the list. There also appears to be a fair number of anomalies in the sorting. That said, we don't depend on any delicate thresholds for "common-ness", so this is not too bad, although certainly nonideal. We're left with about 60,000 words that we can assume actually are words. However, many of these are still not very common.
According to The Economist, the average native English speaking adult knows 20,000 - 35,000 words, 8 year olds know about 10,000, and 4 year olds know about 5,000. Since they gathered this data from their own users, we can probably assume the numbers are inflated. Further, those 20,000 words the adults typically know aren't all going to be exactly the top 20,000 words in the English language. Finally, we want to use words that are easy to remember, not just words users are mildly acquinted with, so we definitely want to use a lower bar than this data would suggest. Let's take the 8 year old count of 10,000.
The last thing we need to do to our word list is remove homophones. I checked for repeat pronunciations in our 10,000 long list of words by binary searching CMUDict's list of pronunciations and removing the less common words of each repeated pronuniation. We were left with 8067 words.
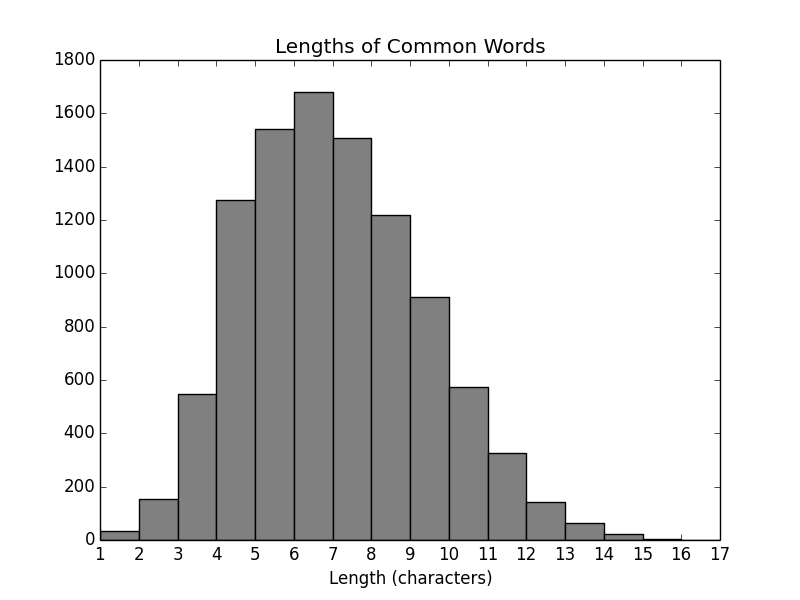
Now, we need to consider the word lengths. Here is the distribution:

The original solution put a length cap at 6, perhaps because when all passwords must be 6 words long, having too many long words would make the password unusably long. Our implementation will not have a fixed number of words per password, so we do not need to ensure all our words are short. How, then, do we decide how many words to use? We know we at least need to meet the recommended minimum password length, 12 characters. We also know that we want the password to be as long as the user is able to remember. I don't feel comfortable saying I know what that length is better than the user, so that part will be interactive.
Oh - I almost forgot to mention the bonus feature: it's free! (as it should be - there isn't even CSS)
Note: This is insecure on Safari and IE. See inline documentation for details.